一、简介
B-tree即B树,B即Balanced(平衡)的意思。B树是为了实现高效的磁盘存取而设计的多叉平衡搜索树,多用于数据库中。B树的启发来源于二叉查找树,二叉查找树的特点是每个非叶子节点都只有两个孩子节点。这种结构会造成当数据量非常大时,二叉查找树的高度非常大,搜索算法从根节点向下搜索时,需要访问的节点数会变多,如果这些节点信息存储在外存储器(磁盘)中,每访问一个节点,就相当于进行了一次I/O操作,而频繁的I/O操作会降低查询的效率。
注:从外部存储器读取信息,大致有两步:
-
找到存储这个数据(节点)对应的磁盘页面,需要依靠磁臂转动,找到对应的磁道。这是一个机械化的过程,所以耗时长。
-
把数据读进内存,并实施运算,这个过程较快。
所以要想提高效率,就要减少磁盘I/O的次数,所以我们要在磁盘页面上多存储一些信息,所以B树就是扩展每个节点的信息,降低树的高度。
B树的说明:
-
B树的阶:节点的最多子节点个数。比如2-3树的阶是3,2-3-4树的阶是4。
-
在B树上,关键字集合分布在整棵树中,即叶子节点和非叶子节点都存放数据。搜索有可能在非叶子节点结束。
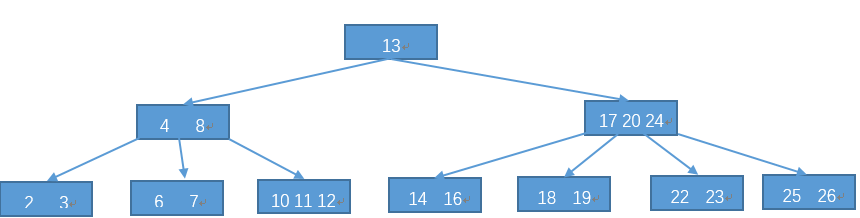
图、4阶B树
一棵m阶B树满足下列条件:
-
每个节点至多有m棵子树;
-
除根节点外,其他分支节点至少有ceil(m/2)棵子树;根节点至少有两棵子树(除非B树只包含一个节点)
-
有j个孩子节点的非叶节点有j−1个关键字,关键字按非降序排列;
-
所有叶子节点具有相同的深度,这也说明B树是平衡的,B-tree的名字也是这样来的
在搜索B树时,很明显,访问节点(即读取磁盘)的次数与树的高度呈正比,而B树与二叉查找树相比,虽然高度都是对数级的,但是显然B树中底数比2大。因此,和二叉树相比,极大地减少了磁盘读取的次数。
二、搜索算法
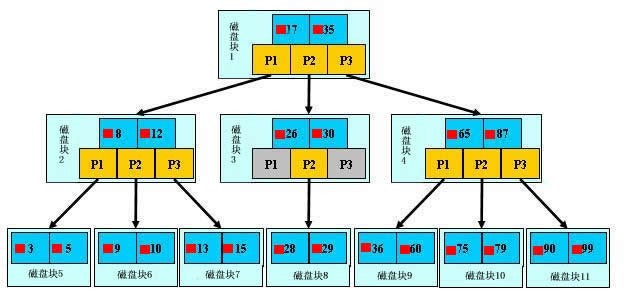
搜索关键字的29的文件的过程如下:
-
从根节点开始,读取根节点信息,根节点有2个关键字:17和35。因为17 < 29 < 35,所以找到指针P2指向的子树,也就是磁盘块3(第1次I/0操作)
-
读取当前节点信息,当前节点有2个关键字:26和30。26 < 29 < 30,找到指针P2指向的子树,也就是磁盘块8(第2次I/0操作)
-
读取当前节点信息,当前节点有2个关键字:28和29。找到了!(第3次I/0操作)
同样的操作,如果使用平衡二叉搜索树,那么需要至少4次I/O操作。这种优势会随着节点数的增加而更加明显。另外,因为B树节点中的关键字都是排序好的,在节点中的信息被读入内存之后,可以采用二分查找,更进一步减少了读入内存之后的计算时间。由此说明对于外存数据结构来说,I/O次数是其查找信息中最大的时间消耗,而我们要做的所有努力就是尽量在搜索过程中减少I/O操作的次数。
三、B+树
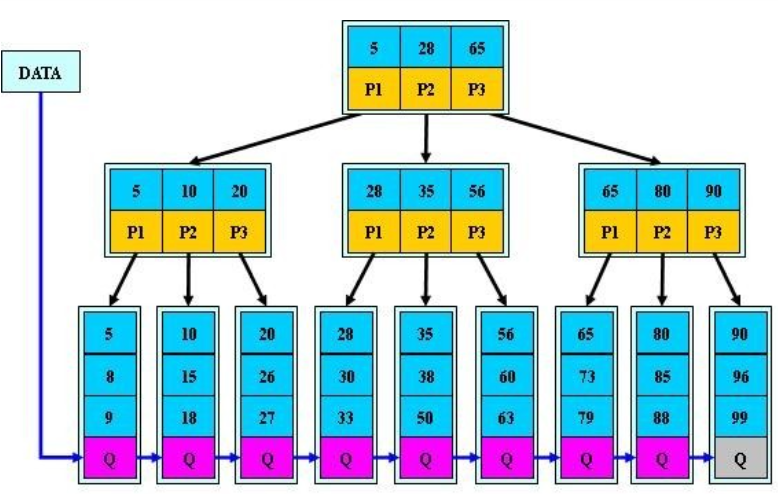
B+树的说明:
-
B+树的搜索算法和B树的区别在于B+树只有在到达叶子节点才命中(B树可以在非叶子节点命中);
-
B+树所有的关键字都出现在叶子节点的链表中(数据只能在叶子节点),并且链表中的关键字 (数据)恰好是有序的;
-
B+树的非叶子节点相当于是叶子节点的索引,它更适合文件索引系统。
问题:为什么B+树比B树更适合文件索引系统和数据库系统?
-
B+树的内部节点(非叶子节点)不保存具体的数据,相比于B树的内部节点更小。故相同容量的磁盘能容纳的内部节点数目更多,磁盘I/O的读写次数也会降低;
-
B+树查询必须查找到叶子节点,B树只要匹配到即可而不用管元素位置(B树最好情况下查找到根节点,最坏情况下查找到叶子结点,所说性能很不稳定),因此B+树查找更稳定;
-
在数据库中基于范围的查询是非常频繁的,B+树首先通过二分查找,找到范围下限,然后遍历叶子节点链表直至找到上限;而B树首先二分查找到范围下限,在不断通过中序遍历,直到查找到范围的上限。
-
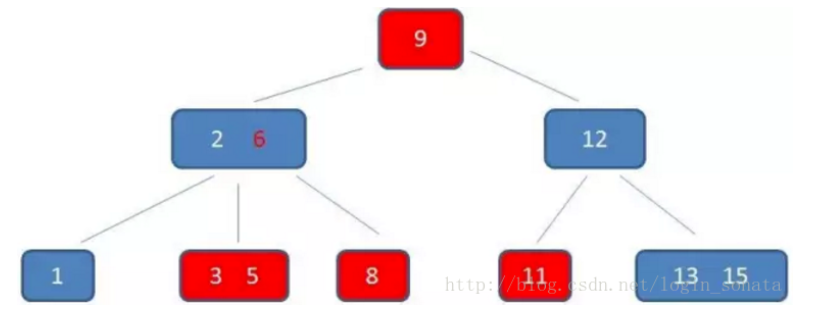
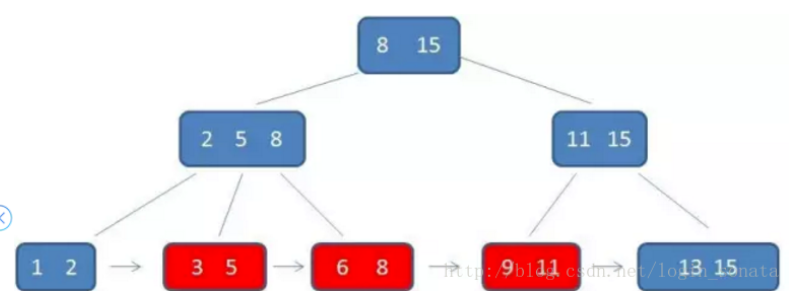
B* 树的介绍
B*树是B+树的变体,在B+树的非根和非叶子节点之间增加指向兄弟的指针。(非叶子结点关键字个数至少为(2/3)*M,即块的最低使用率为2/3,而B+树的块儿的最低使用率为1/2)
有n棵子树的结点中含有n个关键字,每个关键字不保存数据,只用来索引。
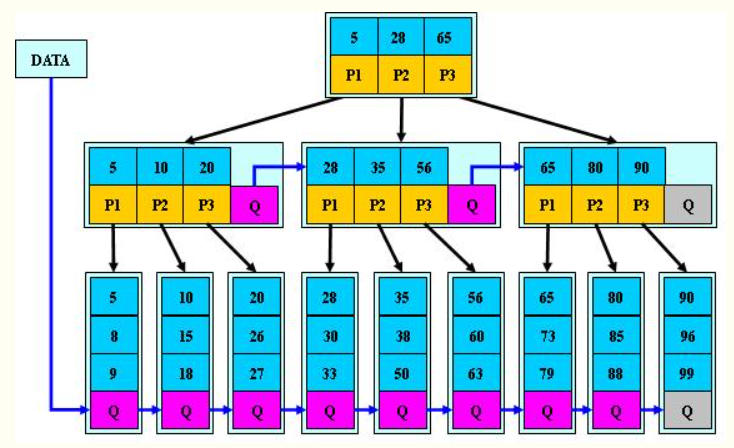
注:B*树分配新节点的概率比B+树要低(B+:当一个结点满时,分配一个新的结点;B*:当一个结点满时,如果它的下一个兄弟结点未满,那么将一部分数据移到兄弟结点中),空间使用率要高(因为每一个块儿的使用率都不是百分之百)。
作者:Ryanjie
出处:http://www.cnblogs.com/ryanjan/
本文版权归作者和博客园所有,欢迎转载。转载请在留言板处留言给我,且在文章标明原文链接,谢谢!
如果您觉得本篇博文对您有所收获,觉得我还算用心,请点击右下角的 [推荐],谢谢!
